線形混合効果モデルの作成
library(lme4) library(lmerTest) library(ggplot2) library(sjPlot) library(sjmisc) ###### ## Data # 2条件×2条件で複数のitemを学習した際の交互作用を見たい。 # 従来は2 × 2 ANOVAを使用。 # 反復測定デザインでの線形混合効果モデル # 従属変数がordinalの場合は一般化線形モデル ###### ## Model Description # model.1: Fixed Slope and Intercept (通常の重回帰分析) model.1 <- lm(time ~ context + task + context : task, data = dat) # model.2: Fixed Slope and Random Intercept model.2 <- lmer(time ~ context * task + (1 | pid) + (1 | item), data = dat) # model.3: Random Slope and Intercept for Participant model.3 <- lmer(time ~ context * task + (context * task | pid) + (1 | item), data = dat) # model.4: Random Slope and Intercept for Item model.4 <- lmer(time ~ context * task + (1 | pid) + (context * task | item), data = dat) # model.5: Random Slope and Intercept model.5 <- lmer(time ~ context * task + (context * task | pid) + (context * task | item), data = dat) # model.6: Random Slope and Fixed Intercept model.6 <- lmer(time ~ context * task + (0 + context * task | pid) + (0 + context * task | item), data = dat)
結果の出力
# model.5のresult
# 推定は制限付き最尤法 (REstricted Maximum Likelihood: REML)
Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
Random effects:
Groups Name Variance Std.Dev. Corr
pid (Intercept) 47092.55330 217.0081872
contextInference 50916.21911 225.6462256 0.5078033
taskL2 Encoding 119031.08661 345.0088211 -0.9420790 -0.7317704
contextInference:taskL2 Encoding 28409.22954 168.5503769 -0.4110683 -0.9849593 0.6299649
item (Intercept) 4325.32673 65.7672162
contextInference 64765.47703 254.4906227 -0.3634969
taskL2 Encoding 3073.53653 55.4394853 -0.2236544 0.9892944
contextInference:taskL2 Encoding 85287.52427 292.0402785 0.2757869 -0.9957147 -0.9985507
Residual 135505.00395 368.1100433
Number of obs: 468, groups: pid, 39; item, 12
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 1111.4737935 62.0879817 19.0270620 17.90159 2.3017e-13 ***
contextInference 234.0348502 101.4480998 13.4981795 2.30694 0.037490 *
taskL2 Encoding -145.8921141 79.2168372 36.4956415 -1.84168 0.073660 .
contextInference:taskL2 Encoding -215.7250504 121.0971969 14.4739459 -1.78142 0.095832 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
モデル選択
## ANOVAによるモデル選択 (AIC)
# AICに有意差がない場合は最もシンプルなモデルを選択
anova(model.2, model.3, model.4, model.5)
Models:
model2: time ~ context * task + (1 | pid) + (1 | item)
model3: time ~ context * task + (context * task | pid) + (1 | item)
model4: time ~ context * task + (1 | pid) + (context * task | item)
model5: time ~ context * task + (context * task | pid) + (context * task | item)
npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
model2 7 6998.220645 7027.259923 -3492.110323 6984.220645
model3 16 6993.191945 7059.567438 -3480.595973 6961.191945 23.02870 9 0.0061322 **
model4 16 6997.952820 7064.328313 -3482.976410 6965.952820 0.00000 0 1.0000000
model5 25 6996.968969 7100.680677 -3473.484485 6946.968969 18.98385 9 0.0253306 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
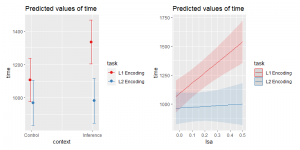
結果の可視化
## plot
# Fixed-effectのみを描画する場合はtype = "eff"
# Interactionを描画する場合はtype = "int"
# Fixed-effectがカテゴリー変数の場合
p1 <-
plot_model(
model.a, type = "int", facet.grid = F,
title = "", fill.alpha = 0.8, geom.size = 1, show.ci = T
)
# Fixed-effectが連続変数の場合
p2 <-
plot_model(
model.b, type = "int", facet.grid = F,
title = "", fill.alpha = 0.8, geom.size = 1, show.ci = T
)
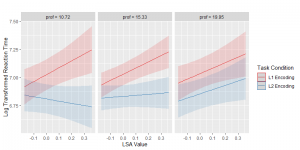
# Three-Way Interaction (Mean±1SD法)
p3 <-
plot_model(
model.c, type = "int", facet.grid = F,
title = "", legend.title = "Task Condition",
fill.alpha = 0.8, geom.size = 1, show.ci = T, mdrt.values = "meansd"
)
p3 + labs(x = "LSA Value", y = "Log Transformed Reaction Time")